Revisiting autoencoders for speech representation learning

Revisiting autoencoders for speech representation learning

“The deep artificial neural networks are inspired from the hierarchical structure of the human brain. Therefore, questioning the neural networks to learn robust, generalizable representations (abstractions) just like the human brain is not absurd, but challenging. However, revisiting fundamentals can be helpful.”

Today, with the advances in deep learning, we can work with deep(er) neural networks. However, as these architectures get deeper and hence more complex, we tend to approach these architectures as black boxes, which leads to losing the valuable theoretical insights.

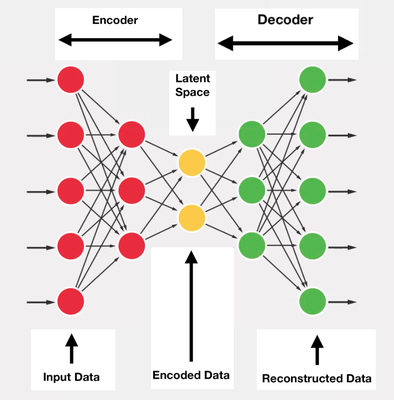
To reclaim these insights and to design compact yet powerful neural networks for learning meaningful representations from speech, we suggest revisiting the autoencoders. The overall idea of an autoencoder is to learn a projection from high-dimensional input data to a lower-dimensional representation space such that the input data samples can be approximately reconstructed from the lower-dimensional representations. Even though the main objective of the autoencoder is to reconstruct its input, under certain constraints, it can still learn useful, interpretable representations in its lower-dimensional representation space.

To elaborate on an exemplar constraint that guides the autoencoder for learning useful representations, we can simply examine the relation of autoencoder and principal component analysis (PCA), which has been acknowledged before. It is known that if an undercomplete autoencoder (Figure1 ) uses linear activation function with the mean square criterion, its weights span the same subspace as the principal components from PCA. However, linear autoencoders can struggle to learn useful lower-dimensional representation of the data, especially when the data is nonlinearly spread in the high-dimensional space.

The better computational capabilities of nonlinear autoencoders can indeed be very useful in practice. Unfortunately, their training can be seriously dragged by local minima in the error surface. Initializing nonlinear autoencoders with PCA loading vectors can help their training to converge faster and better, also enhancing their modeling capacity.