Gradient-based Methods for Deep Model Interpretability

Gradient-based Methods for Deep Model Interpretability

In his research work, Idiap student, Suraj Srinivas proposes gradient-based methods for characterizing model behavior for the purposes of knowledge transfer and post-hoc model interpretation. Broadly, gradients capture the variation of some output feature of the model upon unit variation of an input feature, and thus encodes the local model behavior while being agnostic to the underlying model architectural choices.

Srinivas’ first contribution is to propose a sample-efficient method to mimic the behavior of a pre-trained teacher model with an untrained student model using gradient information. He interprets this approach as an efficient alternative to data augmentation used with canonical knowledge transfer approaches, where noise is added to the inputs. He applies this to distillation and a transfer-learning task, where he shows improved performance for small datasets.

 

 


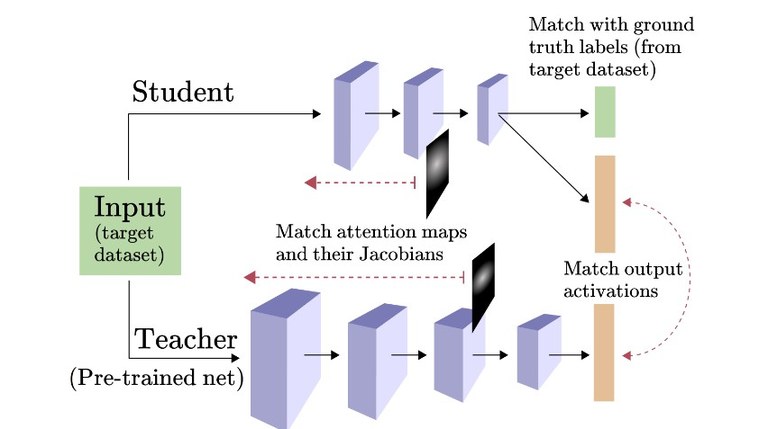
The second contribution of this research is to propose a novel saliency method to visualize the input features that are most relevant for predictions made by a given model. Srinivas first proposes the full-gradient representation, which satisfies a property called completeness, which provably cannot be satisfied by gradient-based saliency methods. Based on this, he proposes an approximate saliency map representation called FullGrad which naturally captures the information within a model across feature hierarchies. His experimental results show that FullGrad captures model behavior better than other saliency methods.


Srinivas’ final contribution is to take a step back and ask why input-gradients are informative for standard neural network models in the first place, especially when their structure may as well be arbitrary. His analysis here reveals that for a subset of gradient-based saliency maps, the map relies not on the underlying discriminative model p(y | x) but on a hidden density model p(x | y) implicit within softmax-based discriminative models. Thus Srinivas finds that the reason input-gradients are informative is due to the alignment of the implicit density model with that of the ground truth density, which he verifies experimentally.

 

More Information