User Guide¶
Methods in the bob.measure module can help you to quickly and easily
evaluate error for multi-class or binary classification problems. If you are
not yet familiarized with aspects of performance evaluation, we recommend the
following papers and book chapters for an overview of some of the implemented
methods.
Bengio, S., Keller, M., Mariéthoz, J. (2004). The Expected Performance Curve. International Conference on Machine Learning ICML Workshop on ROC Analysis in Machine Learning, 136(1), 1963–1966.
Martin, A., Doddington, G., Kamm, T., Ordowski, M., & Przybocki, M. (1997). The DET curve in assessment of detection task performance. Fifth European Conference on Speech Communication and Technology (pp. 1895-1898).
Li, S., Jain, A.K. (2005), Handbook of Face Recognition, Chapter 14, Springer
Overview¶
A classifier is subject to two types of errors, either the event one wishes to detect is rejected (false negative) or an the noise or background one wishes to discard is accepted (false positive). A possible way to measure the detection performance is to use the Half Total Error Rate (HTER), which combines the False Negative Rate (FNR) and the False Positive Rate (FPR) and is defined in the following formula:
where \(\mathcal{D}\) denotes the dataset used. Since both the FPR and the FNR depends on the threshold \(\tau\), they are strongly related to each other: increasing the FPR will reduce the FNR and vice-versa. For this reason, results are often presented using either a Receiver Operating Characteristic (ROC) or a Detection-Error Tradeoff (DET) plot, these two plots basically present the FPR versus the FNR for different values of the threshold. Another widely used measure to summarise the performance of a system is the Equal Error Rate (EER), defined as the point along the ROC or DET curve where the FPR equals the FNR.
However, it was noted in by Bengio et al. (2004) that ROC and DET curves may be misleading when comparing systems. Hence, the so-called Expected Performance Curve (EPC) was proposed and consists of an unbiased estimate of the reachable performance of a system at various operating points. Indeed, in real-world scenarios, the threshold \(\tau\) has to be set a priori: this is typically done using a development set (also called cross-validation set). Nevertheless, the optimal threshold can be different depending on the relative importance given to the FPR and the FNR. Hence, in the EPC framework, the cost \(\beta \in [0;1]\) is defined as the trade-off between the FPR and FNR. The optimal threshold \(\tau^*\) is then computed using different values of \(\beta\), corresponding to different operating points:
where \(\mathcal{D}_{d}\) denotes the development set and should be completely separate to the evaluation set \(\mathcal{D}\).
Performance for different values of \(\beta\) is then computed on the evaluation set \(\mathcal{D}_{t}\) using the previously derived threshold. Note that setting \(\beta\) to 0.5 yields to the Half Total Error Rate (HTER) as defined in the first equation.
Note
Most of the methods available in this module require as input a set of 2
numpy.ndarray objects that contain the scores obtained by the
classification system to be evaluated, without specific order. Most of the
classes that are defined to deal with two-class problems. Therefore, in this
setting, and throughout this manual, we have defined that the negatives
represents the impostor attacks or false class accesses (that is when a
sample of class A is given to the classifier of another class, such as class
B) for of the classifier. The second set, referred as the positives
represents the true class accesses or signal response of the classifier. The
vectors are called this way because the procedures implemented in this module
expects that the scores of negatives to be statistically distributed to
the left of the signal scores (the positives). If that is not the case,
one should either invert the input to the methods or multiply all scores
available by -1, in order to have them inverted.
The input to create these two vectors is generated by experiments conducted
by the user and normally sits in files that may need some parsing before
these vectors can be extracted. While it is not possible to provide a parser
for every individual file that may be generated in different experimental
frameworks, we do provide a parser for a generic two columns format
where the first column contains -1/1 for negative/positive and the second column
contains score values. Please refer to the documentation of
bob.measure.load.split() for more details.
In the remainder of this section we assume you have successfully parsed and loaded your scores in two 1D float64 vectors and are ready to evaluate the performance of the classifier.
Verification¶
To count the number of correctly classified positives and negatives you can use the following techniques:
>>> # negatives, positives = parse_my_scores(...) # write parser if not provided!
>>> T = 0.0 #Threshold: later we explain how one can calculate these
>>> correct_negatives = bob.measure.correctly_classified_negatives(negatives, T)
>>> FPR = 1 - (float(correct_negatives.sum())/negatives.size)
>>> correct_positives = bob.measure.correctly_classified_positives(positives, T)
>>> FNR = 1 - (float(correct_positives.sum())/positives.size)
We do provide a method to calculate the FPR and FNR in a single shot:
>>> FPR, FNR = bob.measure.fprfnr(negatives, positives, T)
The threshold T is normally calculated by looking at the distribution of
negatives and positives in a development (or validation) set, selecting a
threshold that matches a certain criterion and applying this derived threshold
to the evaluation set. This technique gives a better overview of the
generalization of a method. We implement different techniques for the
calculation of the threshold:
Threshold for the EER
>>> T = bob.measure.eer_threshold(negatives, positives)
Threshold for the minimum HTER
>>> T = bob.measure.min_hter_threshold(negatives, positives)
Threshold for the minimum weighted error rate (MWER) given a certain cost \(\beta\).
>>> cost = 0.3 #or "beta" >>> T = bob.measure.min_weighted_error_rate_threshold(negatives, positives, cost)
Note
By setting cost to 0.5 is equivalent to use
bob.measure.min_hter_threshold().
Important
Often, it is not numerically possible to match the requested criteria for
calculating the threshold based on the provided scores. Instead, the closest
possible threshold is returned. For example, using
bob.measure.eer_threshold() will not give you a threshold where
\(FPR == FNR\). Hence, you cannot report \(FPR\) or \(FNR\)
instead of \(EER\); you should report \((FPR+FNR)/2\). This
is also true for bob.measure.far_threshold() and
bob.measure.frr_threshold(). The threshold returned by those functions
does not guarantee that using that threshold you will get the requested
\(FPR\) or \(FNR\) value. Instead, you should recalculate using
bob.measure.fprfnr().
Note
Many functions in bob.measure have an is_sorted parameter, which defaults to False, throughout.
However, these functions need sorted positive and/or negative scores.
If scores are not in ascendantly sorted order, internally, they will be copied – twice!
To avoid scores to be copied, you might want to sort the scores in ascending order, e.g., by:
>>> negatives.sort()
>>> positives.sort()
>>> t = bob.measure.min_weighted_error_rate_threshold(negatives, positives, cost, is_sorted = True)
>>> assert T == t
Identification¶
For identification, the Recognition Rate is one of the standard measures.
To compute recognition rates, you can use the bob.measure.recognition_rate() function.
This function expects a relatively complex data structure, which is the same as for the CMC below.
For each probe item, the scores for negative and positive comparisons are computed, and collected for all probe items:
>>> rr_scores = []
>>> for probe in range(10):
... pos = numpy.random.normal(1, 1, 1)
... neg = numpy.random.normal(0, 1, 19)
... rr_scores.append((neg, pos))
>>> rr = bob.measure.recognition_rate(rr_scores, rank=1)
For open set identification, according to Li and Jain (2005) there are two different error measures defined.
The first measure is the bob.measure.detection_identification_rate(), which counts the number of correctly classified in-gallery probe items.
The second measure is the bob.measure.false_alarm_rate(), which counts, how often an out-of-gallery probe item was incorrectly accepted.
Both rates can be computed using the same data structure, with one exception.
Both functions require that at least one probe item exists, which has no according gallery item, i.e., where the positives are empty or None:
(continued from above…)
>>> for probe in range(10):
... pos = None
... neg = numpy.random.normal(-2, 1, 10)
... rr_scores.append((neg, pos))
>>> dir = bob.measure.detection_identification_rate(rr_scores, threshold = 0, rank=1)
>>> far = bob.measure.false_alarm_rate(rr_scores, threshold = 0)
Confidence interval¶
A confidence interval for parameter \(x\) consists of a lower estimate \(L\), and an upper estimate \(U\), such that the probability of the true value being within the interval estimate is equal to \(\alpha\). For example, a 95% confidence interval (i.e. \(\alpha = 0.95\)) for a parameter \(x\) is given by \([L, U]\) such that
The smaller the test size, the wider the confidence interval will be, and the greater \(\alpha\), the smaller the confidence interval will be.
The Clopper-Pearson interval, a common method for calculating
confidence intervals, is function of the number of success, the number of trials
and confidence
value \(\alpha\) is used as bob.measure.utils.confidence_for_indicator_variable().
It is based on the cumulative probabilities of the binomial distribution. This
method is quite conservative, meaning that the true coverage rate of a 95%
Clopper–Pearson interval may be well above 95%.
For example, we want to evaluate the reliability of a system to identify registered persons. Let’s say that among 10,000 accepted transactions, 9856 are true matches. The 95% confidence interval for true match rate is then: .. doctest:: python
>>> numpy.allclose(bob.measure.utils.confidence_for_indicator_variable(9856, 10000),(0.98306835053282549, 0.98784270928084694))
True
meaning there is a 95% probability that the true match rate is inside \([0.983, 0.988]\).
Plotting¶
An image is worth 1000 words, they say. You can combine the capabilities of Matplotlib with Bob to plot a number of curves. However, you must have that package installed though. In this section we describe a few recipes.
ROC¶
The Receiver Operating Characteristic (ROC) curve is one of the oldest plots in town. To plot an ROC curve, in possession of your negatives and positives, just do something along the lines of:
>>> from matplotlib import pyplot
>>> # we assume you have your negatives and positives already split
>>> npoints = 100
>>> bob.measure.plot.roc(negatives, positives, npoints, color=(0,0,0), linestyle='-', label='test')
>>> pyplot.xlabel('FPR (%)')
>>> pyplot.ylabel('FNR (%)')
>>> pyplot.grid(True)
>>> pyplot.show()
>>> # You can also compute the area under the ROC curve:
>>> bob.measure.roc_auc_score(negatives, positives)
0.8958
You should see an image like the following one:
(Source code, png, hires.png, pdf)
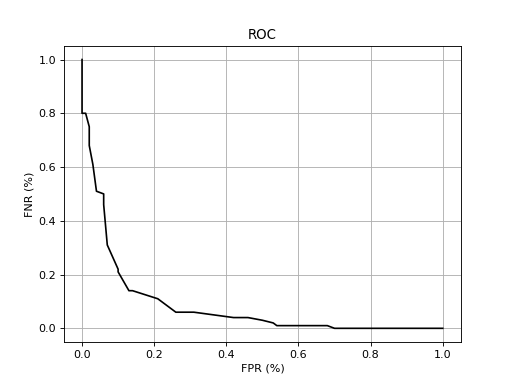
As can be observed, plotting methods live in the namespace
bob.measure.plot. They work like the
matplotlib.pyplot.plot() itself, except that instead of receiving the
x and y point coordinates as parameters, they receive the two
numpy.ndarray arrays with negatives and positives, as well as an
indication of the number of points the curve must contain.
As in the matplotlib.pyplot.plot() command, you can pass optional
parameters for the line as shown in the example to setup its color, shape and
even the label. For an overview of the keywords accepted, please refer to the
Matplotlib’s Documentation. Other plot properties such as the plot title,
axis labels, grids, legends should be controlled directly using the relevant
Matplotlib’s controls.
DET¶
A DET curve can be drawn using similar commands such as the ones for the ROC curve:
>>> from matplotlib import pyplot
>>> # we assume you have your negatives and positives already split
>>> npoints = 100
>>> bob.measure.plot.det(negatives, positives, npoints, color=(0,0,0), linestyle='-', label='test')
>>> bob.measure.plot.det_axis([0.01, 40, 0.01, 40])
>>> pyplot.xlabel('FPR (%)')
>>> pyplot.ylabel('FNR (%)')
>>> pyplot.grid(True)
>>> pyplot.show()
This will produce an image like the following one:
(Source code, png, hires.png, pdf)
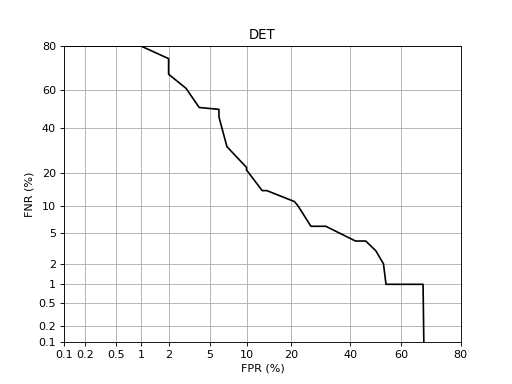
Note
If you wish to reset axis zooming, you must use the Gaussian scale rather
than the visual marks showed at the plot, which are just there for
displaying purposes. The real axis scale is based on the
bob.measure.ppndf() method. For example, if you wish to set the x and y
axis to display data between 1% and 40% here is the recipe:
>>> #AFTER you plot the DET curve, just set the axis in this way:
>>> pyplot.axis([bob.measure.ppndf(k/100.0) for k in (1, 40, 1, 40)])
We provide a convenient way for you to do the above in this module. So,
optionally, you may use the bob.measure.plot.det_axis method like this:
>>> bob.measure.plot.det_axis([1, 40, 1, 40])
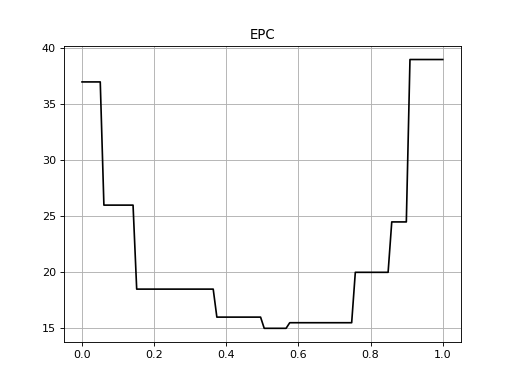
EPC¶
Drawing an EPC requires that both the development set negatives and positives are provided alongside the evaluation set ones. Because of this the API is slightly modified:
>>> bob.measure.plot.epc(dev_neg, dev_pos, test_neg, test_pos, npoints, color=(0,0,0), linestyle='-')
>>> pyplot.show()
This will produce an image like the following one:
(Source code, png, hires.png, pdf)
CMC¶
The Cumulative Match Characteristics (CMC) curve estimates the probability that
the correct model is in the N models with the highest similarity to a given
probe. A CMC curve can be plotted using the bob.measure.plot.cmc()
function. The CMC can be calculated from a relatively complex data structure,
which defines a pair of positive and negative scores per probe:
(Source code, png, hires.png, pdf)
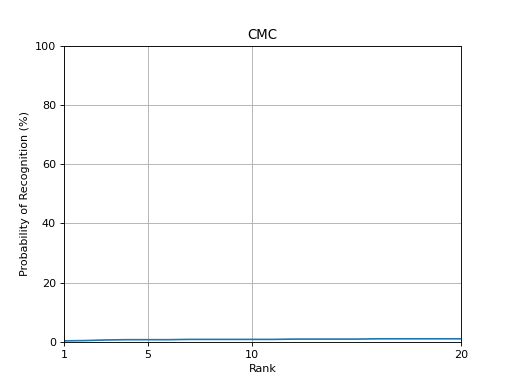
Usually, there is only a single positive score per probe, but this is not a fixed restriction.
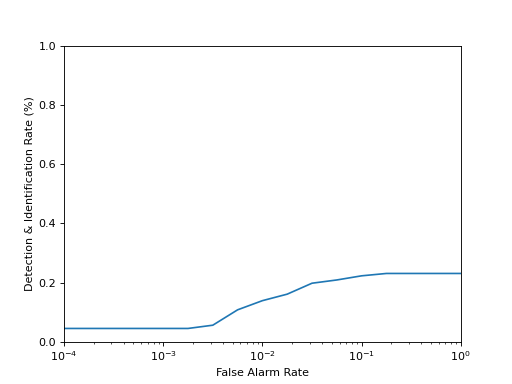
Detection & Identification Curve¶
The detection & identification curve is designed to evaluate open set
identification tasks. It can be plotted using the
bob.measure.plot.detection_identification_curve() function, but it
requires at least one open-set probe, i.e., where no corresponding positive
score exists, for which the FPR values are computed. Here, we plot the
detection and identification curve for rank 1, so that the recognition rate for
FPR=1 will be identical to the rank one bob.measure.recognition_rate()
obtained in the CMC plot above.
(Source code, png, hires.png, pdf)
Fine-tunning¶
The methods inside bob.measure.plot are only provided as a
Matplotlib wrapper to equivalent methods in bob.measure that can
only calculate the points without doing any plotting. You may prefer to tweak
the plotting or even use a different plotting system such as gnuplot. Have a
look at the implementations at bob.measure.plot to understand how to
use the Bob methods to compute the curves and interlace that in the way
that best suits you.
Full applications¶
Commands under bob measure can be used to quickly evaluate a set of
scores and generate plots. We present these commands in this section. The commands
take as input generic 2-column data format as specified in the documentation of
bob.measure.load.split()
Metrics¶
To calculate the threshold using a certain criterion (EER (default) or min.HTER) on a development set and conduct the threshold computation and its performance on an evaluation set, after setting up Bob, just do:
bob measure metrics ./MTest1/scores-{dev,eval} -e -v
[Min. criterion: EER ] Threshold on Development set `./MTest1/scores-dev`: -1.373550e-02
bob.measure@2018-06-29 10:20:14,177 -- WARNING: NaNs scores (1.0%) were found in ./MTest1/scores-dev
bob.measure@2018-06-29 10:20:14,177 -- WARNING: NaNs scores (1.0%) were found in ./MTest1/scores-eval
=================== ================ ================
.. Development Evaluation
=================== ================ ================
False Positive Rate 15.5% (767/4942) 15.5% (767/4942)
False Negative Rate 15.5% (769/4954) 15.5% (769/4954)
Precision 0.8 0.8
Recall 0.8 0.8
F1-score 0.8 0.8
=================== ================ ================
The output will present the threshold together with the FPR, FNR, Precision, Recall, F1-score and HTER on the given set, calculated using such a threshold. The relative counts of FAs and FRs are also displayed between parenthesis.
Note
Several scores files can be given at once and the metrics will be computed
for each of them separatly. Development and evaluation files must be given by
pairs. When evaluation files are provided, --eval flag
must be given.
To evaluate the performance of a new score file with a given threshold, use
--thres:
bob measure metrics ./MTest1/scores-eval -v --thres 0.006
[Min. criterion: user provided] Threshold on Development set `./MTest1/scores-eval`: 6.000000e-03
bob.measure@2018-06-29 10:22:06,852 -- WARNING: NaNs scores (1.0%) were found in ./MTest1/scores-eval
=================== ================
.. Development
=================== ================
False Positive Rate 15.2% (751/4942)
False Negative Rate 16.1% (796/4954)
Precision 0.8
Recall 0.8
F1-score 0.8
=================== ================
You can simultaneously conduct the threshold computation and its performance on an evaluation set:
Note
Table format can be changed using --tablefmt option, the default format
being rst. Please refer to bob measure metrics --help for more details.
Plots¶
Customizable plotting commands are available in the bob.measure module.
They take a list of development and/or evaluation files and generate a single PDF
file containing the plots. Available plots are:
roc(receiver operating characteristic)det(detection error trade-off)epc(expected performance curve)hist(histograms of positive and negatives)
Use the --help option on the above-cited commands to find-out about more
options.
For example, to generate a DET curve from development and evaluation datasets:
$bob measure det -e -v --output "my_det.pdf" -ts "DetDev1,DetEval1,DetDev2,DetEval2"
dev-1.txt eval-1.txt dev-2.txt eval-2.txt
where my_det.pdf will contain DET plots for the two experiments.
Note
By default, det and roc plot development and evaluation curves on
different plots. You can force gather everything in the same plot using
--no-split option.
Note
The --figsize and --style options are two powerful options that can
dramatically change the appearance of your figures. Try them! (e.g.
--figsize 12,10 --style grayscale)
Evaluate¶
A convenient command evaluate is provided to generate multiple metrics and
plots for a list of experiments. It generates two metrics outputs with ERR
and min-HTER criteria along with roc, det, epc, hist plots for each
experiment. For example:
$bob measure evaluate -e -v -l 'my_metrics.txt' -o 'my_plots.pdf' {sys1,sys2}/{dev,eval}
will output metrics and plots for the two experiments (dev and eval pairs) in my_metrics.txt and my_plots.pdf, respectively.