Exemplary Usage¶
In this documentation, exemplary use cases for the Gabor wavelet transform (and related) classes are detailed.
Gabor wavelets¶
The bob.ip.gabor.Wavelet class can be used to create Gabor wavelets.
The parametrization is according to what is explained in detail in [Guenther2011].
The Gabor wavelets by default are in frequency domain.
To create a Gabor wavelet of size (128, 128) with the vertical orientation and frequency \(\frac{\pi}{8}\), you call:
>>> wavelet = bob.ip.gabor.Wavelet(resolution = (128, 128), frequency = (math.pi/2, 0))
To compute the wavelet transform, an image of the same resolution in frequency domain must be present.
To generate an image in frequency domain, one can use the bob.sp.fft() function:
>>> test_image = numpy.zeros((128,128), numpy.uint8)
>>> test_image[32:96, 32:96] = 255
>>> freq_image = bob.sp.fft(test_image.astype(numpy.complex128))
Now, the wavelet transform with the given wavelet can be applied:
>>> transformed_freq_image = wavelet.transform(freq_image)
To get the transformed image in spatial domain, it needs to be transformed back, e.g., using bob.sp.ifft():
>>> transformed_image = bob.sp.ifft(transformed_freq_image)
Please note that the resulting image is complex valued. You can look at its real and its absolute components:
>>> real_image = numpy.real(transformed_image)
>>> abs_image = numpy.abs(transformed_image)
A full working example (including the plotting) is given below:
import numpy
import math
import bob.ip.gabor
import bob.sp
# create exemplary image
image = numpy.zeros((128,128), numpy.uint8)
image[32:96,32:96] = 255
# create Gabor wavelet
wavelet = bob.ip.gabor.Wavelet(resolution = (128, 128), frequency = (math.pi/8., 0))
# compute wavelet transform in frequency domain
freq_image = bob.sp.fft(image.astype(numpy.complex128))
transformed_freq_image = wavelet.transform(freq_image)
transformed_image = bob.sp.ifft(transformed_freq_image)
# get layers of the image
real_image = numpy.real(transformed_image)
abs_image = numpy.abs(transformed_image)
# get the wavelet in spatial domain
spat_wavelet = bob.sp.ifft(wavelet.wavelet.astype(numpy.complex128))
real_wavelet = numpy.real(spat_wavelet)
# align wavelet to show it centered
aligned_wavelet = numpy.roll(numpy.roll(real_wavelet, 64, 0), 64, 1)
# create figure
from matplotlib import pyplot
pyplot.figure(figsize=(20,5))
pyplot.subplot(141)
pyplot.imshow(image, cmap='gray')
pyplot.title("Original image")
pyplot.subplot(142)
pyplot.imshow(aligned_wavelet, cmap='gray')
pyplot.title("Gabor wavelet")
pyplot.subplot(143)
pyplot.imshow(real_image, cmap='gray')
pyplot.title("Real part")
pyplot.subplot(144)
pyplot.imshow(abs_image, cmap='gray')
pyplot.title("Abs part")
pyplot.show()
(Source code, png, hires.png, pdf)
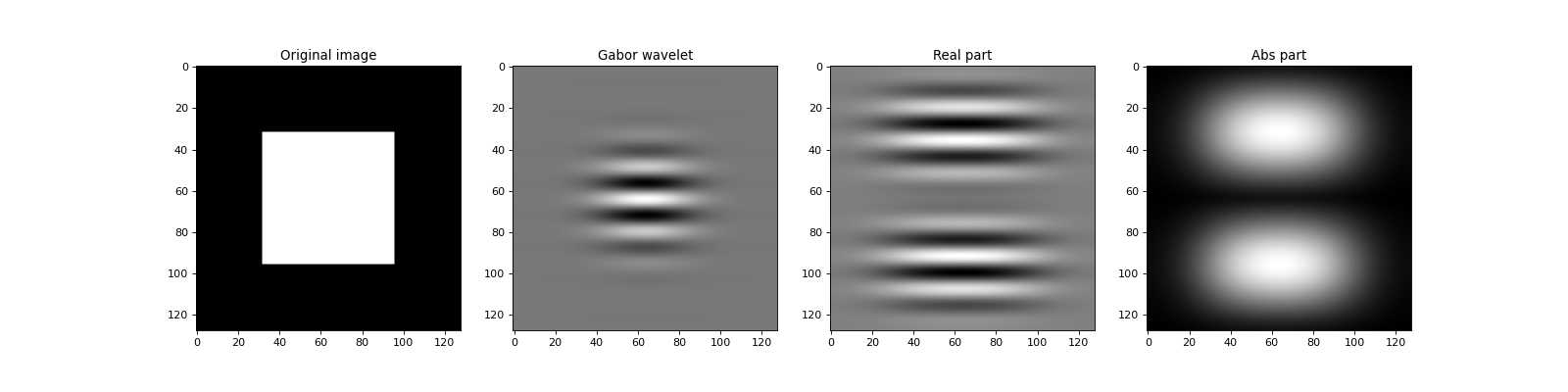
Gabor wavelet transform¶
The bob.ip.gabor.Transform class is performs a Gabor wavelet transform using a discrete family of Gabor wavelets.
The family of Gabor wavelets is composed of wavelets in different scales and orientations.
By default, the family consists of Gabor wavelets in 5 scales and 8 orientations:
>>> gwt = bob.ip.gabor.Transform()
>>> gwt.number_of_scales
5
>>> gwt.number_of_directions
8
>>> gwt.number_of_wavelets
40
When transforming an image, all Gabor wavelets will be applied to it.
In opposition to the bob.ip.gabor.Wavelet class (see above), the parameters to the bob.ip.gabor.Transform expects all input and output images to be in spatial domain:
>>> trafo_image = gwt.transform(test_image)
>>> trafo_image.shape
(40, 128, 128)
>>> trafo_image.dtype
dtype('complex128')
The result is a 40 layer image that contains the complex-valued results of the transform. A few of these results (together with the according wavelets) can be seen here:
import numpy
import math
import bob.ip.gabor
import bob.sp
# create test image
image = numpy.zeros((128,128), numpy.float)
image[32:96,32:96] = 255
# compute the Gabor wavelet transform
gwt = bob.ip.gabor.Transform()
trafo_image = gwt(image)
# create image representation of all Gabor wavelets in frequency domain
wavelets_image = numpy.zeros((128,128), numpy.float)
# compute the sum over all wavelets
for wavelet in gwt.wavelets:
wavelets_image += wavelet.wavelet
# align the wavelets so that the center is in the image center
aligned_wavelets_image = numpy.roll(numpy.roll(wavelets_image, 64, 0), 64, 1)
# create figure
import matplotlib
# plot wavelets image
from matplotlib import pyplot
pyplot.figure(figsize=(20,10))
pyplot.subplot(121)
pyplot.imshow(aligned_wavelets_image, cmap='gray')
pyplot.title("Family of Gabor wavelets in frequency domain")
pyplot.xticks((0, 32, 64, 96, 128), ("$-\pi$", "$-\pi/2$", "$0$", "$\pi/2$", "$\pi$"))
pyplot.yticks((0, 32, 64, 96, 128), ("$-\pi$", "$-\pi/2$", "$0$", "$\pi/2$", "$\pi$"))
pyplot.gca().invert_yaxis()
# plot the results of the transform for some wavelets
for scale in (0,2,4):
for direction in (0,2,4):
pyplot.subplot(3,6,4+scale*3+direction//2)
pyplot.imshow(numpy.real(trafo_image[scale*gwt.number_of_directions+direction]), cmap='gray')
pyplot.title("Scale %d, direction %d" % (scale, direction))
pyplot.gca().invert_yaxis()
pyplot.show()
(Source code, png, hires.png, pdf)
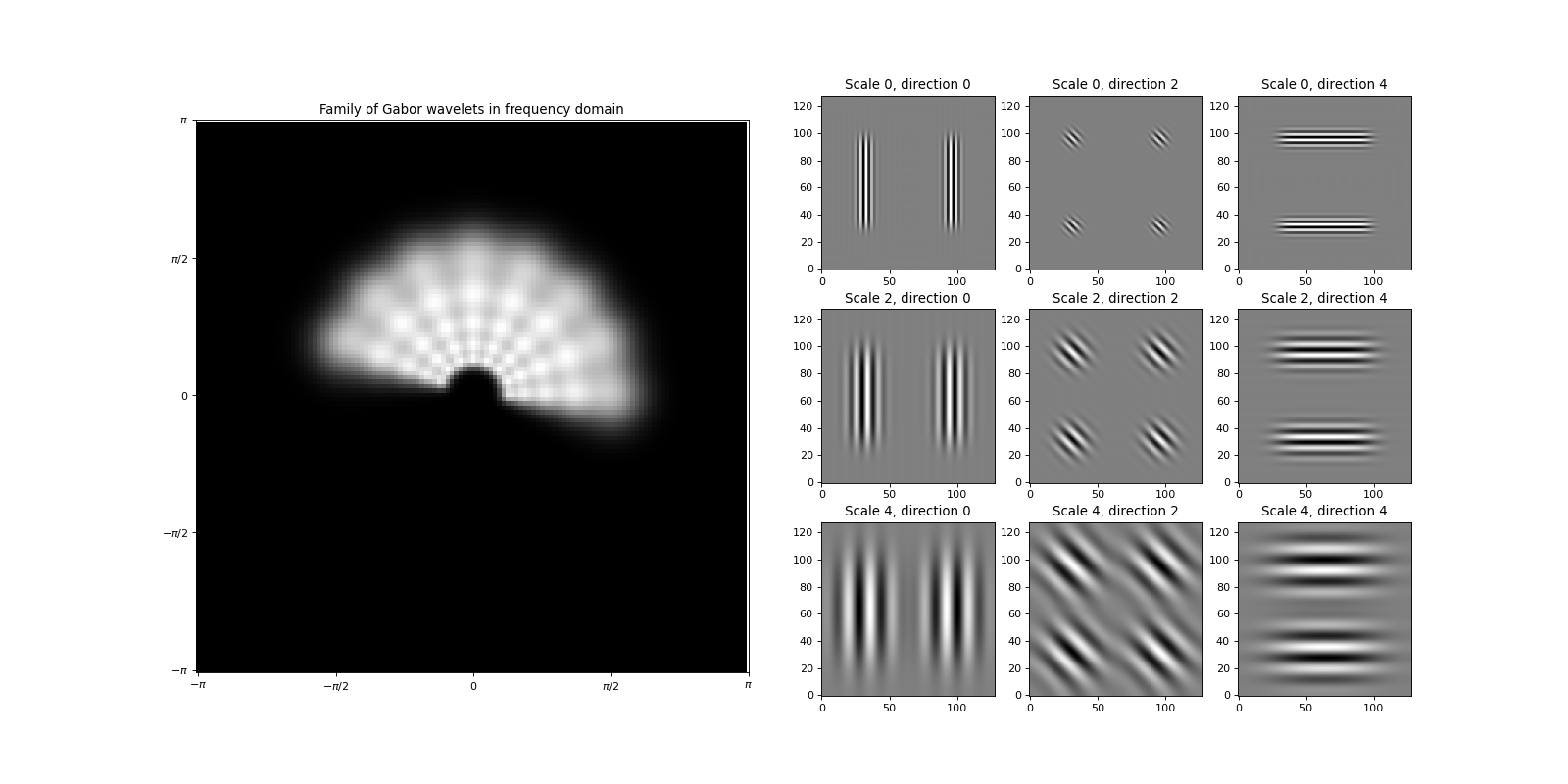
The first row displays the Gabor wavelet family in frequency domain can be obtained by (cf. Figure 2.2 of [Guenther2011]).
Gabor jet and their similarities¶
A Gabor jet bob.ip.gabor.Jet is the collection of the (complex valued) responses of all Gabor wavelets of the family at a certain point in the image.
The Gabor jet is a local texture descriptor, that can be used for various applications.
To extract the texture from the right eye landmark from a facial image, one can simply call:
>>> image = bob.io.base.load(bob.io.base.test_utils.datafile("testimage.hdf5", 'bob.ip.gabor'))
>>> gwt = bob.ip.gabor.Transform()
>>> trafo_image = gwt(image)
>>> eye_jet = bob.ip.gabor.Jet(trafo_image, (177, 131))
>>> len(eye_jet)
40
One of these applications is to locate the texture in a given image.
E.g., one might locate the position of the eye by scanning over the whole image.
At each position in the image, the similarity between the reference Gabor jet and the Gabor jet at this location is computed using a bob.ip.gabor.Similarity.
For this computation, both traditional [Wiskott1997] and innovative [Guenther2012] similarity functions can be used.
A more detailed description of implemented Gabor jet similarity functions can be obtained in the documentation of bob.ip.gabor.Similarity.
In fact, since the texture descriptor is stable against small shifts, only every 4th pixel will be extracted, and the original offset position is not included:
import numpy
import bob.io.base
import bob.io.base.test_utils
import bob.ip.gabor
# load test image
image = bob.io.base.load(bob.io.base.test_utils.datafile("testimage.hdf5", 'bob.ip.gabor'))
# perform Gabor wavelet transform on image
gwt = bob.ip.gabor.Transform()
trafo_image = gwt(image)
# extract Gabor jet at right eye location
pos = (177, 131)
eye_jet = bob.ip.gabor.Jet(trafo_image, pos)
# compute similarity field over the whole image
cos_sim = bob.ip.gabor.Similarity("ScalarProduct")
disp_sim = bob.ip.gabor.Similarity("Disparity", gwt)
cos_image = numpy.zeros(((image.shape[0]+1)//4, (image.shape[1]+1)//4))
disp_image = numpy.zeros(((image.shape[0]+1)//4, (image.shape[1]+1)//4))
# .. re-use the same Gabor jet object to avoid memory allocation
image_jet = bob.ip.gabor.Jet()
for y in range(2, image.shape[0], 4):
for x in range(2, image.shape[1], 4):
image_jet.extract(trafo_image, (y,x))
cos_image[y//4,x//4] = cos_sim(image_jet, eye_jet)
disp_image[y//4,x//4] = disp_sim(image_jet, eye_jet)
# plot the image and the similarity map side-by-side
from matplotlib import pyplot
pyplot.figure(figsize=(20,7))
pyplot.subplot(131)
pyplot.imshow(image, cmap='gray')
pyplot.plot(pos[1], pos[0], "gx", markersize=20, mew=4)
pyplot.axis([0, image.shape[1], image.shape[0], 0])
#pyplot.axis("scaled")
pyplot.title("Original image")
pyplot.subplot(132)
pyplot.imshow(cos_image, cmap='jet')
pyplot.title("Similarities (cosine)")
pyplot.subplot(133)
pyplot.imshow(disp_image, cmap='jet')
pyplot.title("Similarities (disparity)")
pyplot.show()
(Source code, png, hires.png, pdf)
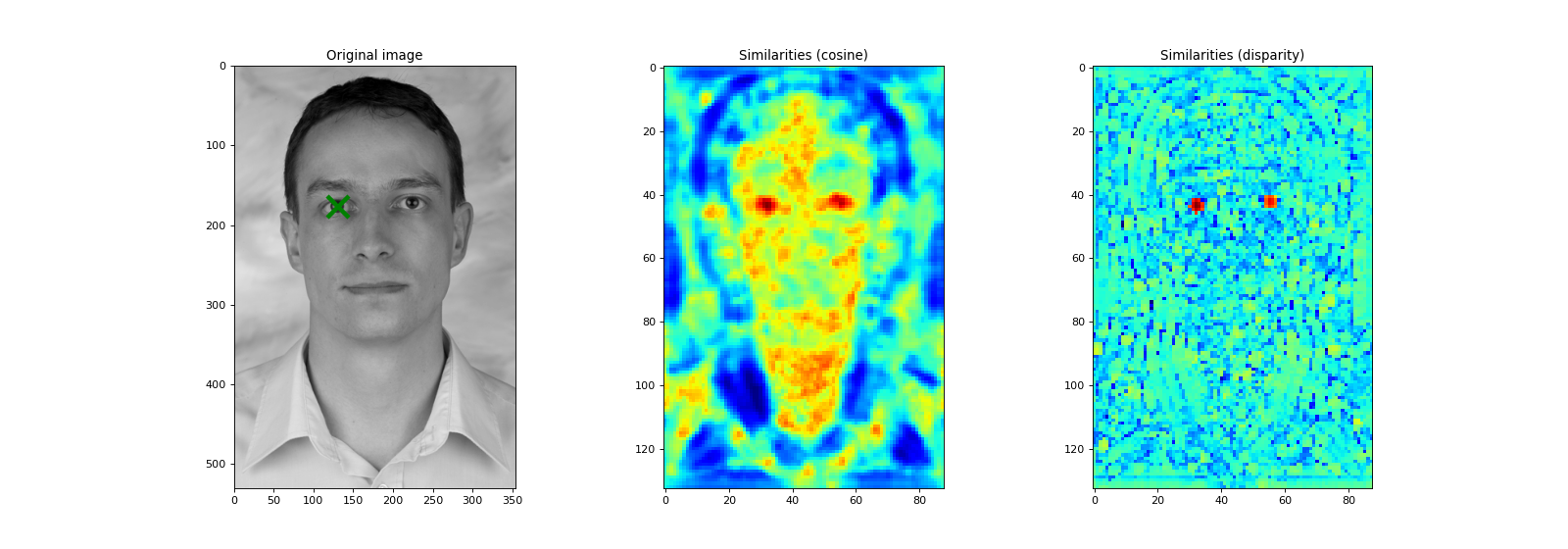
As can be clearly seen, both eye regions have high similarities with both similarity functions (remember, we are searching with only the right eye Gabor jet).
The difference is in the other regions of the face.
While the traditional cosine similarity (aka. 'ScalarProduct') has high similarity values all over the image, the novel 'Disparity' similarity highlights specifically the eye regions.
Gabor jet disparities¶
The disparity similarity function has even another use case.
Given a reference Gabor jet extracted at a reference location, the spatial offset of a given other Gabor jet can be computed using the bob.ip.gabor.Similarity.disparity() function.
It can estimate the disparity (difference in spatial position) between two Gabor jets, as long as they stem from a similar region:
>>> disp_sim = bob.ip.gabor.Similarity("Disparity", gwt)
>>> pos = (231, 173)
>>> dist = (5, 6)
>>> jet1 = bob.ip.gabor.Jet(trafo_image, pos)
>>> jet2 = bob.ip.gabor.Jet(trafo_image, (pos[0] - dist[0], pos[1] - dist[1]))
>>> print ("%1.3f, %1.3f" % tuple(disp_sim.disparity(jet1, jet2)))
4.816, 5.683
Hence, this function can be used to localize landmarks. In the following example, we use the Gabor jet at the nose tip as a reference, and we compute the disparity from Gabor jets extracted from around that offset position. We plot these disparities as arrows:
import bob.ip.gabor
import bob.io.base
import bob.io.base.test_utils
# load test image
image = bob.io.base.load(bob.io.base.test_utils.datafile("testimage.hdf5", 'bob.ip.gabor'))
# perform Gabor wavelet transform on image
gwt = bob.ip.gabor.Transform(number_of_scales=9)
trafo_image = gwt(image)
# extract reference Gabor jet at nose tip location
pos = (228, 173)
reference_jet = bob.ip.gabor.Jet(trafo_image, pos)
r = 40
# extract test region from image (for displaying purposes
region = image[pos[0]-r:pos[0]+r+1, pos[1]-r:pos[1]+r+1]
# display test region
from matplotlib import pyplot
pyplot.figure(figsize=(7,7))
pyplot.imshow(region, cmap='gray')
pyplot.axis([0, region.shape[1]-1, region.shape[0]-1, 0])
pyplot.xticks(range(0,81,20), range(-40,41,20))
pyplot.yticks(range(0,81,20), range(-40,41,20))
# create a disparity-based similarity function
similarity = bob.ip.gabor.Similarity("Disparity", gwt)
cmap=pyplot.get_cmap("jet")
# compute disparities of all gabor jets around the current location
for y in range(-30, 31, 6):
for x in range(-30, 31, 6):
if x or y:
# extract Gabor jet at location
jet = bob.ip.gabor.Jet(trafo_image, (pos[0] + y, pos[1] + x))
# compute the similarity between the two jets
sim = similarity(reference_jet, jet)
# get the disparity of the two jets
disp = similarity.last_disparity
# normalize similarity from range [-1, 1] to range [0,1] to obtain a proper color coding
color = cmap((sim + 1.) / 2.)
# plot the disparity as an arrow from the current location, with the given similarity as a color code
pyplot.arrow(x+r, y+r, disp[1], disp[0], color = color, head_width=2)
pyplot.show()
(Source code, png, hires.png, pdf)
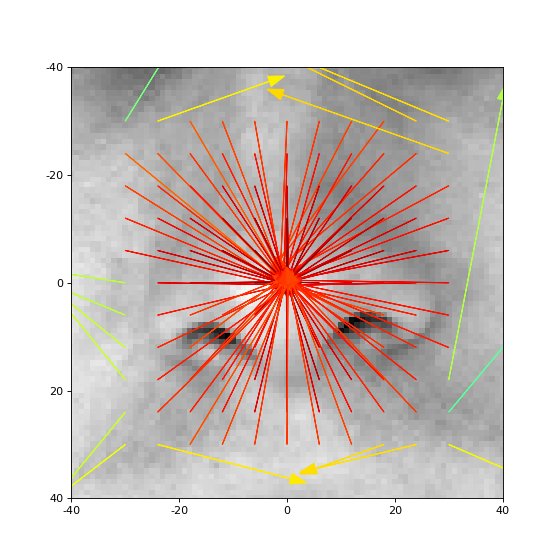
As you can see, inside a certain region, all arrows point (more or less) to the right location, and the similarity value is quite high (color red).
Closer to the offset point, the disparities point more precisely to the right location.
Outside of that region, disparities are more or less random, and also the similarity values are low.
Theoretically, the size of the region can be increased, e.g., using the bob.ip.gabor.Transform.number_of_scales or bob.ip.gabor.Transform.k_max parameters.Anyways, after a certain size is passed, the disparities become imprecise.
In this small example, we used the reference and target Gabor jets from the same image, but there is no real need for that.
When you extract the reference Gabor jet from one image, and compute the disparity to a Gabor jet from another image, you can get a good estimation of the correct location of the underlying image texture.
This can be used for precise landmark localization, e.g., when trying to locate the facial landmarks in a novel image.
An implementation of that technique was used in the Elastic Bunch Graph Matching (EBGM) [Wiskott1997].
A statistical extension of the EBGM, which was used in [Guenther2011], uses the statistics of Gabor jets instead of computing the disparity for all jets individually.
The Gabor jet statistics are implemented in the bob.ip.gabor.JetStatistics class, which also provides a function bob.ip.gabor.JetStatistics.disparity() to compute the disparity.
Gabor graphs¶
Finally, graphs of Gabor jets can be used to identify a person.
The bob.ip.gabor.Graph class is designed to extract Gabor jets at regular grid positions in the image.
Particularly for face recognition, the grid graph can be aligned to eye positions, but also a regular grid can be created by specifying the first and the last node, as well as the step width:
>>> graph = bob.ip.gabor.Graph(first=(100,100), last=(image.shape[0]-100, image.shape[1]-100), step = (20, 20))
>>> graph.number_of_nodes
136
>>> graph.nodes[0]
(100, 100)
>>> graph.nodes[135]
(420, 240)
This graph can be used to extract Gabor jets from a Gabor transformed image:
>>> jets = graph.extract(trafo_image)
>>> len(jets)
136
When graphs are extracted from two facial images, the average similarity of the Gabor jets can be used to define, whether two images contain the same identities. A complete example on the AT&T database can be found in the bob.example.faceverify package.